Conservação de energia

Energia Cinética

A energia cinética é a energia produzida pela movimentação dos corpos. Do grego o termo "cinética" significa "movimento" enquanto "energia" corresponde a trabalho. Grosso modo, a energia cinética corresponde ao trabalho dos corpos realizado através do movimento. No SI (Sistema Internacional) a unidade de medida da energia cinética é o Joule (J).

Fórmula da Energia Cinética

Para calcular a energia cinética dos corpos utiliza-se a equação abaixo:

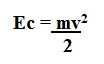
Onde:

Ec: energia cinética, também pode ser representada pela letra K

M: massa do corpo

V: velocidade do corpo

A partir disso, conclui-se que quanto maior a massa de um corpo maior será sua velocidade; logo, a energia cinética será determinada pela ação dos corpos em movimento sendo que quanto maior sua velocidade maior será a energia cinética produzida.

A Cinemática é o ramo da Física que descreve o movimento dos corpos (principalmente os lineares e circulares), determinando seu deslocamento, velocidade, tempo e aceleração. O Joule (J), unidade de medida da energia cinética, corresponde a uma homenagem ao cientista inglês James Prescott Joule (1818-1889).

A energia presente nos corpos dando a eles a capacidade de realizar trabalho é chamada de Energia Potencial.

Quando está relacionada aos trabalhos da força peso, a energia armazenada nos corpos é chamada Energia Potencial Gravitacional e quando está associada a uma força elástica é Energia Potencial Elástica.

A unidade de medida da Energia Potencial é Joule.

Energia Potencial Gravitacional

O objeto de massa m se desloca a uma altura h, indo da posição B para A.

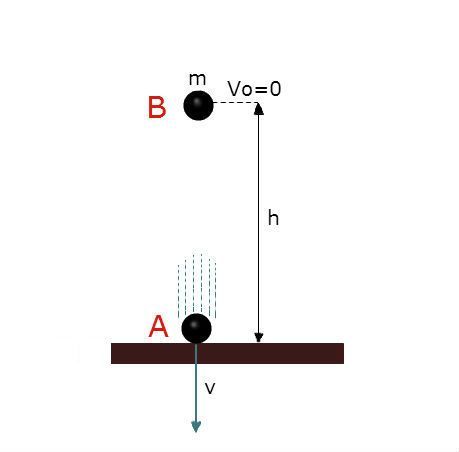
É a energia que um objeto possui devido à sua posição em um campo gravitacional e é medida pelo trabalho realizado pelo seu peso para ir de uma posição (mais elevada) à outra (mais abaixo).

Assim, é necessário usar uma força para elevar um objeto até uma determinada altura, nesse ponto mais alto o objeto tem maior energia potencial, quando o objeto desce libera sua energia, que será convertida em energia cinética.

Portanto, a energia potencial gravitacional do objeto está associada com a sua posição (altura relativa a um ponto de referência), com a sua massa e com a força da gravidade.

Considerando que a força exigida para elevar um objeto é igual ao seu peso, a energia potencial gravitacional é igual ao seu peso (m x g) multiplicado pela altura h a que foi elevado.

A força da gravidade varia com a altura, na superfície da Terra a diferença é muito pequena, assim considera-se a aceleração da gravidade como uma constante, de 9,8m/s2, em qualquer parte.

A fórmula então é: EPg = mgh

​Exercício Resolvido

Um objeto de 2Kg é lançado da janela de um prédio de 10 m. Considerando a aceleração da gravidade local g=10m/s2. Qual é a Energia Potencial Gravitacional do objeto?

Resolução: A energia potencial gravitacional (EPg) está relacionada com o peso do objeto (massa x gravidade) e a altura do seu deslocamento. Então, calculamos a EPg usando os valores do enunciado.

EPg =m x g x h , onde m=2Kg g=10m/s2 e h= 10m

EPg = 2 x10 x10

EPg = 200 J.

Energia Potencial Elástica

Para lançar a flecha (corpo de massa m), o elástico do arco sofre uma deformação (medida por x) passando da posição de equilíbrio A para B.

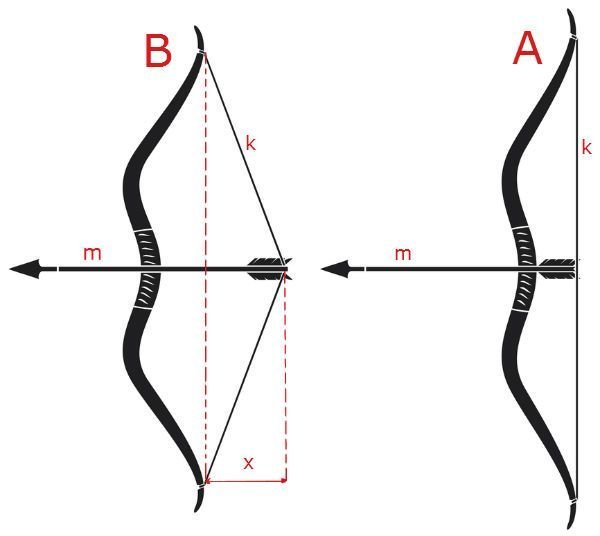
Um corpo elástico é aquele que sofre uma deformação, produzida por uma força externa, passando de uma posição A (não deformado) para uma posição B (deformado) e recupera sua forma e tamanho original, voltando a posição inicial.

Portanto a posição de equilíbrio corresponde à posição em que o elástico ou a mola não está nem comprimida, nem esticada, é a sua posição natural.

A Energia Potencial Elástica está relacionada com o trabalho realizado pela força elástica do corpo para ir da posição deformada B para a posição inicial A.

É considerado no sistema elástico o corpo de massa m, uma constante da força elástica k e o comprimento x (a medida da deformação, quando o corpo passa da posição A para a posição B).

A fórmula é EPe = Kx2/2.

Exercício

Uma mola de constante K=5000 N/m é comprimida por uma distância de 10 cm. Qual é a energia potencial elástica nela armazenada?

A energia potencial elástica depende apenas da constante elástica da mola k e de sua deformação x. Então, calculamos a energia potencial usando os valores do enunciado.

EPe =Kx2/2 , onde K=5000 N/m e x= 10cm ⇒ 0,1m

EPe = (5000 x 0,12)/2 ⇒ (5000 x 0,01)/2 ⇒ 50/2

EPe = 25 J.

À medida que o patinador sobe a rampa, sua energia potencial aumenta e a cinética diminui

Desde os primeiros estudos sobre um sistema físico, sabemos que a energia mecânica pode ser modificada, mas nada dela se perde. Por vários anos, diversos trabalhos, nas mais variadas áreas, direcionaram para a formulação de uma lei fundamental denominada lei da conservação da energia. Quando ela é encarada como um dos pilares da construção do universo, nos referimos a ela como Princípio da Conservação da Energia.

Voltemos às forças conservativas: elas foram assim denominadas por causa dessa lei. Sistemas em que apenas as forças conservativas realizam trabalho conservam a energia mecânica (observe que o sistema pode apresentar outras forças, desde que elas não realizem trabalho).

No estudo da mecânica, as forças gravitacional e elástica são caracterizadas como sendo forças conservativas. Então, sistemas nos quais apenas essas duas forças realizam trabalho apresentam a energia mecânica inicial igual à energia mecânica final. Vejamos alguns exemplos:

Suponhamos que temos um ponto material, e que esse ponto material seja lançado para cima, em uma região de vácuo, na superfície da Terra. No decorrer de sua subida, a energia potencial desse ponto material aumenta, enquanto que sua energia cinética diminui de tal forma que a soma entre essas duas energias seja sempre constante. Ao descer, a energia potencial é gradualmente transformada em energia cinética.

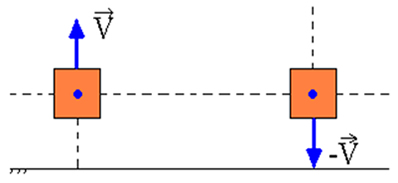
Já em um sistema massa-mola sem atrito, quando o bloco é deslocado do ponto de referência (O) e depois abandonado, verificamos a conservação da energia mecânica em qualquer ponto durante seu movimento oscilatório.

Se houver trabalho de forças não conservativas, a energia mecânica não se conservará, isto é, ela pode diminuir ou aumentar. As forças não conservativas cujo trabalho provoca diminuição da energia mecânica são denominadas forças dissipativas. É o caso da força de atrito de escorregamento e da força de resistência do ar.

Vamos supor que um corpo em movimento possua, num ponto A, energia cinética , energia potencial gravitacional e energia elástica . Ao passar por um outro ponto, B, ele possuirá energia cinética , energia potencial gravitacional  e energia potencial elástica . Se apenas forças conservativas realizarem trabalho, a lei da conservação da energia mecânica garante que:

E_cA +E_p(g)A+E_eA=E_cB+E_p(g)B +E_eB

As situações nas quais o princípio da conservação da energia mecânica é válido são ideais. Rigorosamente, elas são raríssimas. Forças dissipativas, como a resistência do ar e os atritos, são praticamente inevitáveis. Para esses sistemas, o trabalho realizado pelas forças dissipativas corresponde à diferença entre a energia mecânica final e inicial do corpo, desde que o sistema não permita a entrada de energia:

τ_Fdissipativa = E_mf - E_mi

Na equação acima temos:

τ – trabalho da força dissipativa
Em_f – energia mecânica final
Em_i – energia mecânica inicial

Transformação da energia potencial gravitacional

Sabemos que a energia nunca pode ser destruída ou criada (princípio geral da conservação de energia). O que ocorre é que a energia está em constante transformação, se apresentando em diferentes formas.

As usinas hidrelétricas são um bom exemplo de transformação da energia.

A energia potencial gravitacional contida na água de uma represa elevada é convertida em energia cinética, movimentando as pás das turbinas da usina.

No gerador o movimento rotatório da turbina se converte em energia elétrica.